费马点定理的证明与补充
定理的证明
定理推广
费马点结论
以下内容可以不看,因为本人第一次头条发文章,数学类文章,公式经常被系统识别为图片,实在难以编辑,故把自己word里复制在下面,跟上文完全相同----------------------------------------.
费马点定理的证明与补充
1.三角形三个内角均小于120°的情况:
·费马点定理 :如果在△ABC 内角均小于120°,P 为平面内任意一点,若点O 对于三边的张角都是120°,则≤(仅当O 、P 重合时取等号)
证明:过A 、B 、C 分别作OA 、OB 、OC 的垂线,设交于、、,如图所示,则O 、B 、C 、四点共圆,由∠BOC =120°,则∠.
同理∠,故△为正三角形.
设其边长为,则
(因为斜线段大于垂线段)
∴≤.
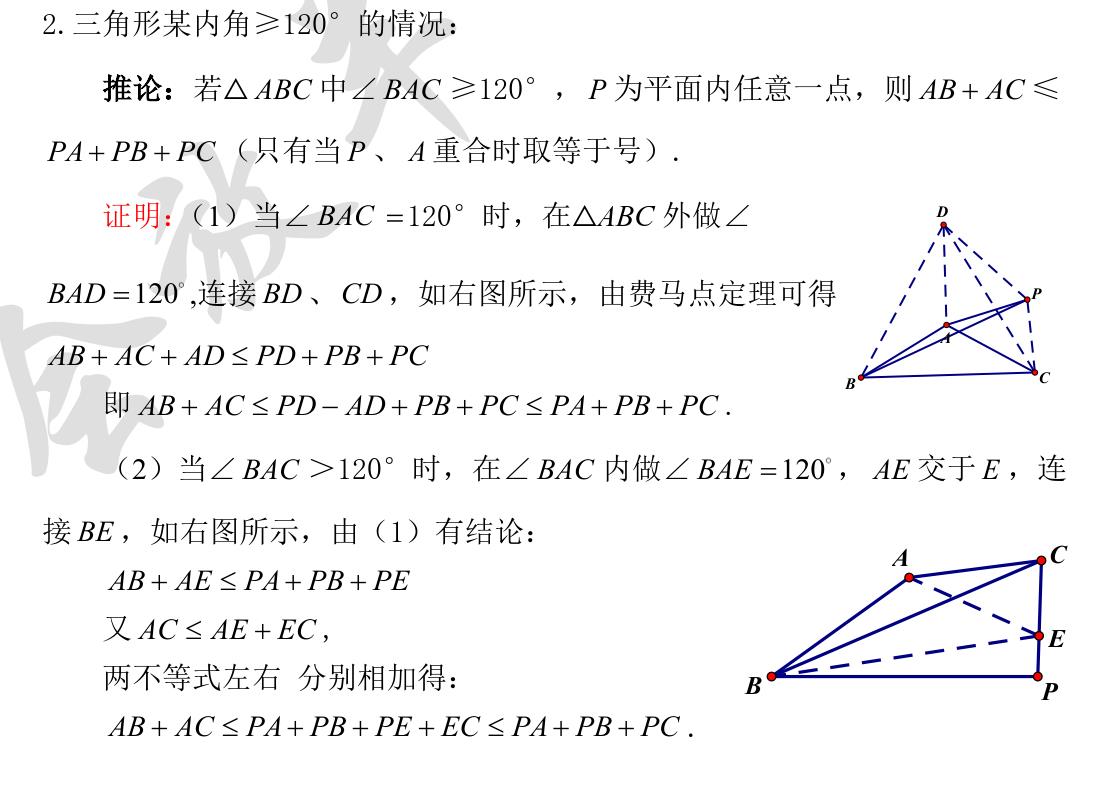
2.三角形某内角≥120°的情况:
推论: 若△中∠≥120°,为平面内任意一点,则≤(只有当、重合时取等于号).
证明:(1)当∠120°时,在△ABC 外做∠,连接、,如右图所示,由费马点定理可得
即.
(2)当∠>120°时,在∠内做∠,交于,连接,如右图所示,由(1)有结论:
又,
两不等式左右 分别相加得:
.
综上所述:若△中∠≥120°,则点为费马点,若内角都小于120°,则三角形内部与三边张角均为120°的点为费马点.
标签:
第五十一期|高清热门二次元美女福利来袭 高清热门二次元美女福利来袭,画质极高,值得收藏一波!!...
SNH48新专辑《公主披风》歌词霸气外露,凸显国内第一女团气 国内女团SNH48新专辑《公主披风》同名主打歌音源于近日发布。这首由JJ林俊杰打造的歌曲,节奏清晰流畅,尤其歌词部分“...
“被情伤过的女人,一定会有三个特点” 不管是男人还是女人,年轻的时候多不免会碰到一两个错误的人,有的从中吸取教训会找到更好的一半,而有些则会受到深深的伤害,伤口一直...
中国内地男演员:赵英俊 赵英俊(原名赵健),1977年7月28日出生于辽宁省抚顺市,中国内地男歌手、音乐制作人、演员。2004年,赵英俊参加了东方卫视的歌唱类真人秀节目《我型我秀...
格伦-罗宾逊三世将参加勇士的试训 HoopsHype记者Michael Scotto报道,联盟消息源透露,自由球员格伦-罗宾逊三世将参加勇士的试训。 罗宾逊今年29岁,曾夺得NBA扣篮大赛冠军。他此前在N...
抖音欧巴欧巴欧巴巴是什么歌 完整版在线试听 欧巴欧巴欧巴巴是什么歌 ?是最近抖音很火很动感的一个DJ,最近好像喜欢DJ的人很多,那么你知道这个歌的名字叫什么吗?一起欣赏试听...
一则无比讽刺的漫画《手机》,开车请不要玩手机 作者@海绵兄...
林依晨的6张照片...
黑白文字壁纸一组黑白文字壁纸背景图锁屏 下角已阅...
猜字谜:守门员(打一字),聪明的你留下你的答案吧 猜字谜:守门员(打一字) 这期答案请看我下篇文章 上期答案 记得关注哦,么么哒!...
“论文” 用英语怎么说? paper/thesis/dissertation 这三个单词又可以表示 论文 thesis 英 [ˈθi:sɪs] 论文,毕业论文 dissertation 英 [ˌdɪsəˈteɪʃn] 专题论文,学位论文 双语例句: Each student h...
重庆地铁27号线 重庆地铁27号线要来啦,这条线路时速将达到140公里每小时,线路两端将和市域铁路衔接,这条地铁给我的感觉就像广州地铁18号线和22号线,本身远期也将和城际铁路贯...
幸福爱人第二部大结局 1. The Twilight Saga: Breaking Dawn will be released as two separate films, Summit Entertainment confirmed. 巅峰娱乐近日证实,《暮光之城》第四部大结局《破晓》将分为上下两部发行....
莆田九龙谷建设高空玻璃天桥 2月9日,我国首座全息7D玻璃天桥在九龙谷4A级景区落成。玻璃天桥长280米、垂直悬空约180米,将为春节旅游增添一项惊险有趣的新项目。图为投用当天,瑜...
你打几分?利拉德晒摄影师拍摄的利拉德7帅照 虎扑11月17日讯 今日,开拓者球员达米安-利拉德更新了Instagram,晒出一张摄影师拍摄的利拉德7的帅照。 2019-20赛季常规赛,利拉德场均出...
开场仅1分钟,小托马斯接触裁判身体被驱逐 开拓者对阵奇才,开场仅仅1分半钟,小托马斯遭到裁判驱逐。 首节还剩10分28秒,小托马斯进攻时遭遇利拉德和卡梅隆-安东尼包夹,争抢时...
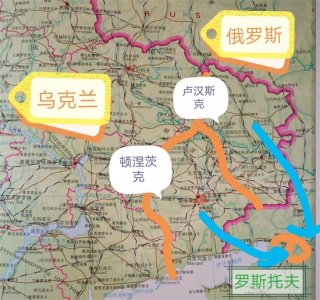
一眼看懂乌克兰东部地区 “乌克兰东部地区”最近引起全球关注。 “顿涅茨克”、“卢汉斯克”这两个地名具体在什么位置? 接收了大批乌东居民的“罗斯托夫”又位于何处? 下面的...
美食介绍-片儿川 简介 片儿川是浙江杭州地区一种著名的汉族传统汤面,面的浇头主要由雪菜、笋片、瘦肉丝组成,鲜美可口。已有百余年历史,最早由杭州老店奎元馆首创,其特色在...
李易峰最新机场饭拍图,生图颜值出众,身穿花衬衫清爽帅气 李易峰最新机场饭拍图,生图颜值出众,身穿花衬衫清爽帅气。...
看图猜成语:两只蜜蜂在打架!十秒内你能猜得对吗? 第一题,两只蜜蜂在打架!这个成语很好猜 第二题,仔细看图,好好思考下! 第三题,这个成语很简单吗?...